Metric unfolding with "munfold" • munfold

The following code demonstrates the use of unfold() with artificial data.

We first create some artificial data of which we know the correct configuration. a1 and a2 are the coordinates of a first group of points, which form a circle (with some very small perturbations added). b1 and b2 are the coordinates of a second group of points, which form a square.

r <- seq(from=0,to=2*pi,length=24)
a1 <- cos(r)*4 + 0.00001*rnorm(r)
a2 <- sin(r)*4 + 0.00001*rnorm(r)
b1 <- c(.5,-.5,-.5,.5)*3 + 5
b2 <- c(.5,.5,-.5,-.5)*3 + 1

Im the next step, we compute the squred distamces between the two groups of points.

D1 <- outer(b1,a1,"-")
D2 <- outer(b2,a2,"-")
Dsq <- D1^2+D2^2

Now we call unfold():

library(munfold)
Dsq.uf<-unfold(Dsq,squared=TRUE)
Dsq.uf


2-dimensional unfolding solution

Group 1: 24 points
Group 2: 4 points

Stress: 7.538699e-22

The printout indicates that unfold() prefers a two-dimensional solution, which fits the observed squared distances perfectly.

The output does not tell us, who well we can recreate the original configuration, so let’s do some plotting.

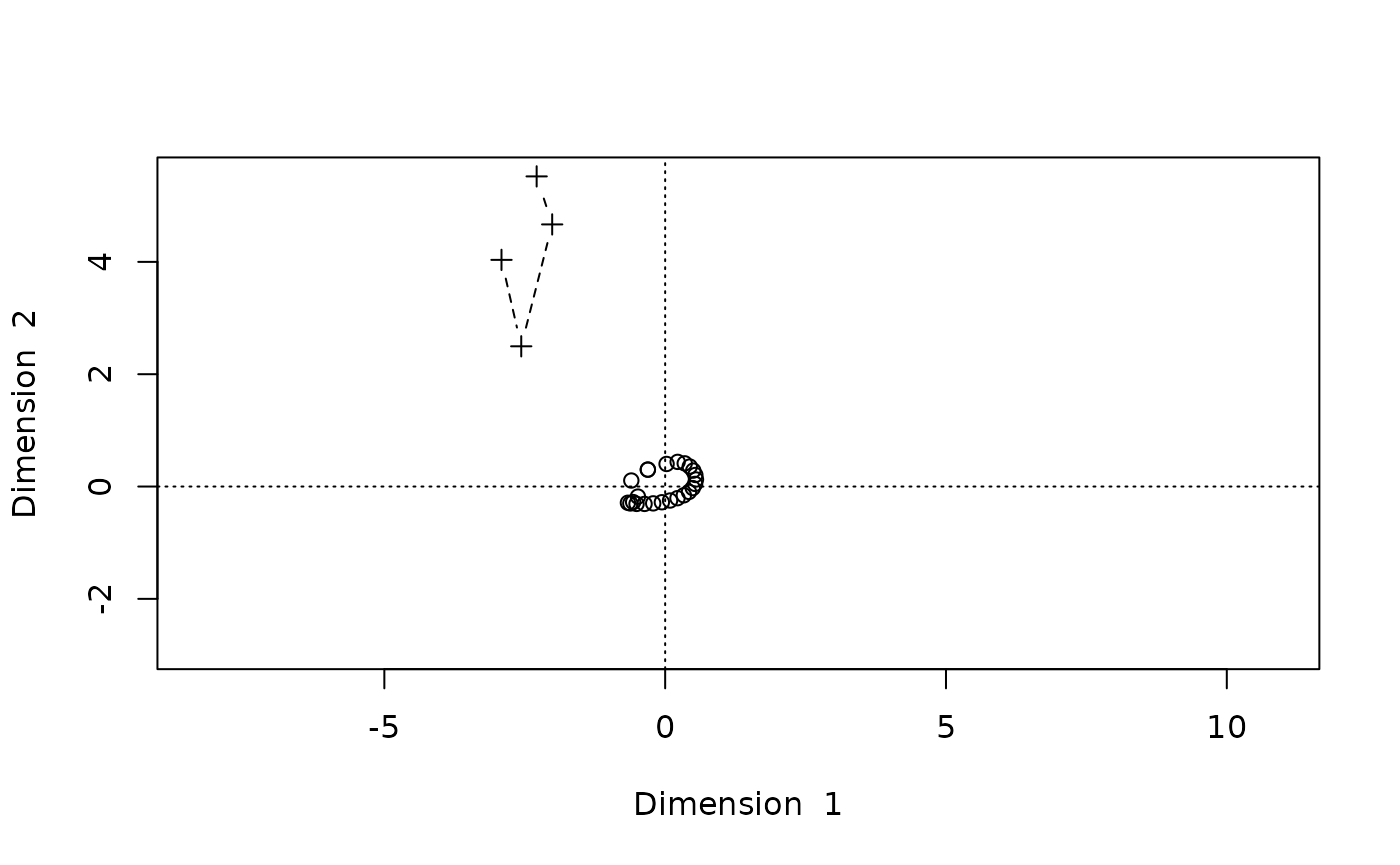
With biplot() we get an illustration of the reconstructed configuration. Second, let’s plot the reconstructed locations of the two groups of points. To enhance the geometric configuration of the points, we require a points-and-line plot by using the argument type="b"

biplot(Dsq.uf,type="b")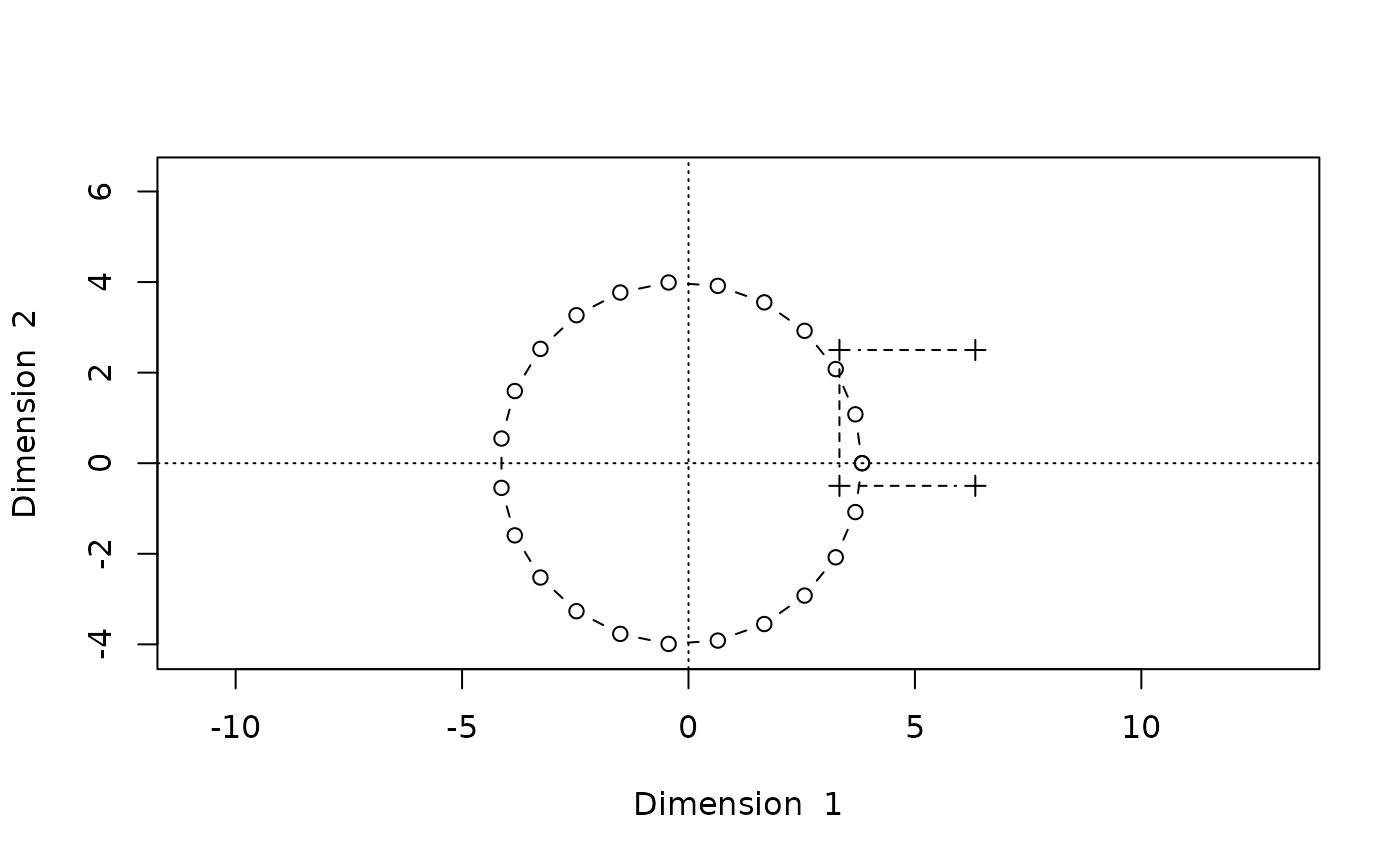

Now let’s compare this with the original configuration, where we need to make sure that all of the original points appear in the plot.

A <- cbind(a1,a2)
B <- cbind(b1,b2)
orig <- rbind(A,B)
xlim <- ylim <- range(orig)#*1.5

plot(A,type="b",pch=1,asp=1,
    xlim=xlim,ylim=ylim,
    xlab="Dimension 1",ylab="Dimension 2")
lines(B,type="b",pch=3,lty=2)
abline(h=0,v=0,lty=3)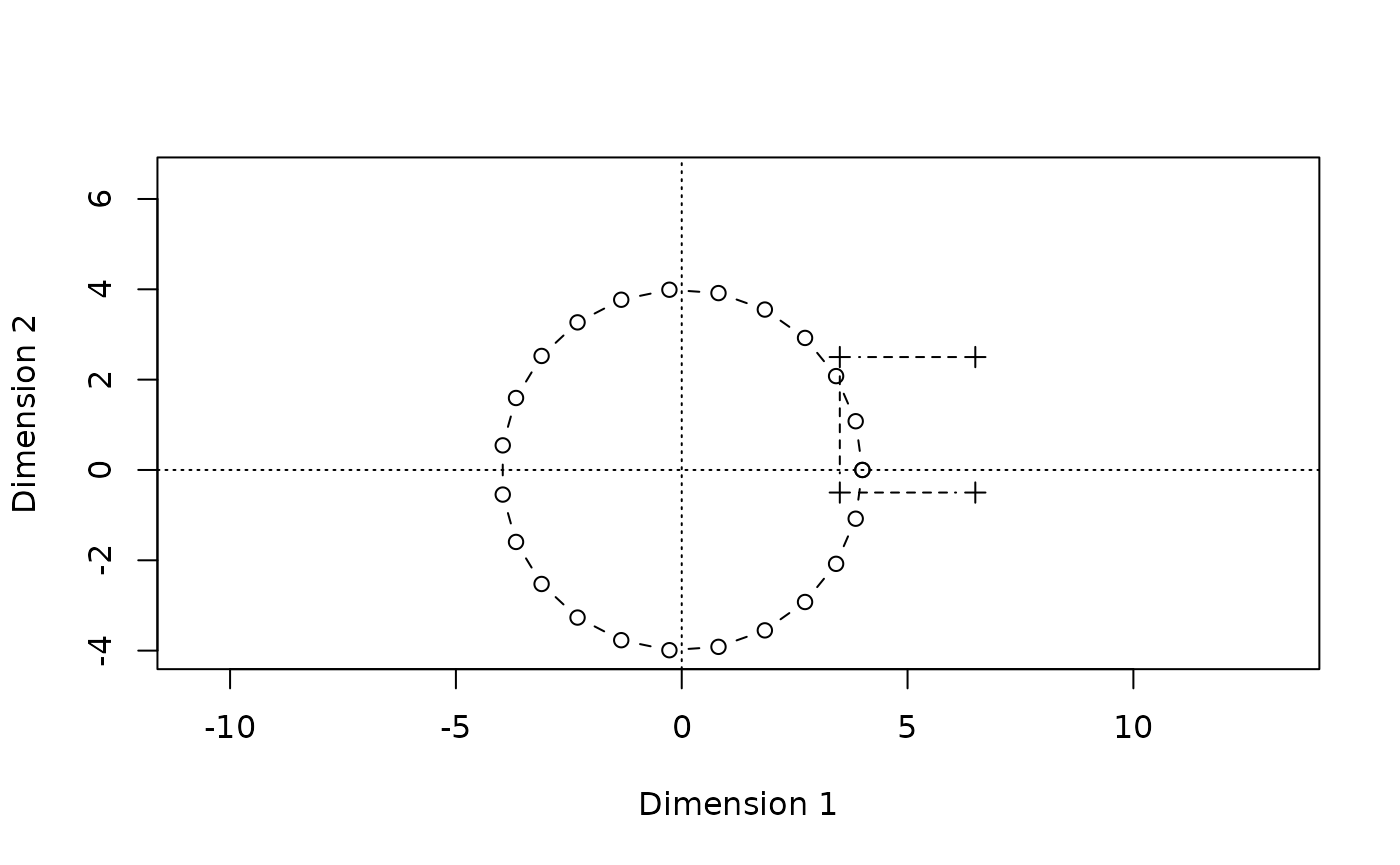

This looks pretty similar, but a comparison will be easier if we put both plots side by side:

oldpar <- par(mfrow=c(1,2))
plot(A,type="b",pch=1,
    xlim=xlim,ylim=ylim,
    xlab="Dimension 1",ylab="Dimension 2",main=expression("Original data"),asp=1)
lines(B,type="b",pch=3,lty=2)
abline(h=0,v=0,lty=3)

biplot(Dsq.uf,type="b",
    xlim=xlim,ylim=ylim,
    main=expression(paste(italic(unfold)," solution")),asp=1)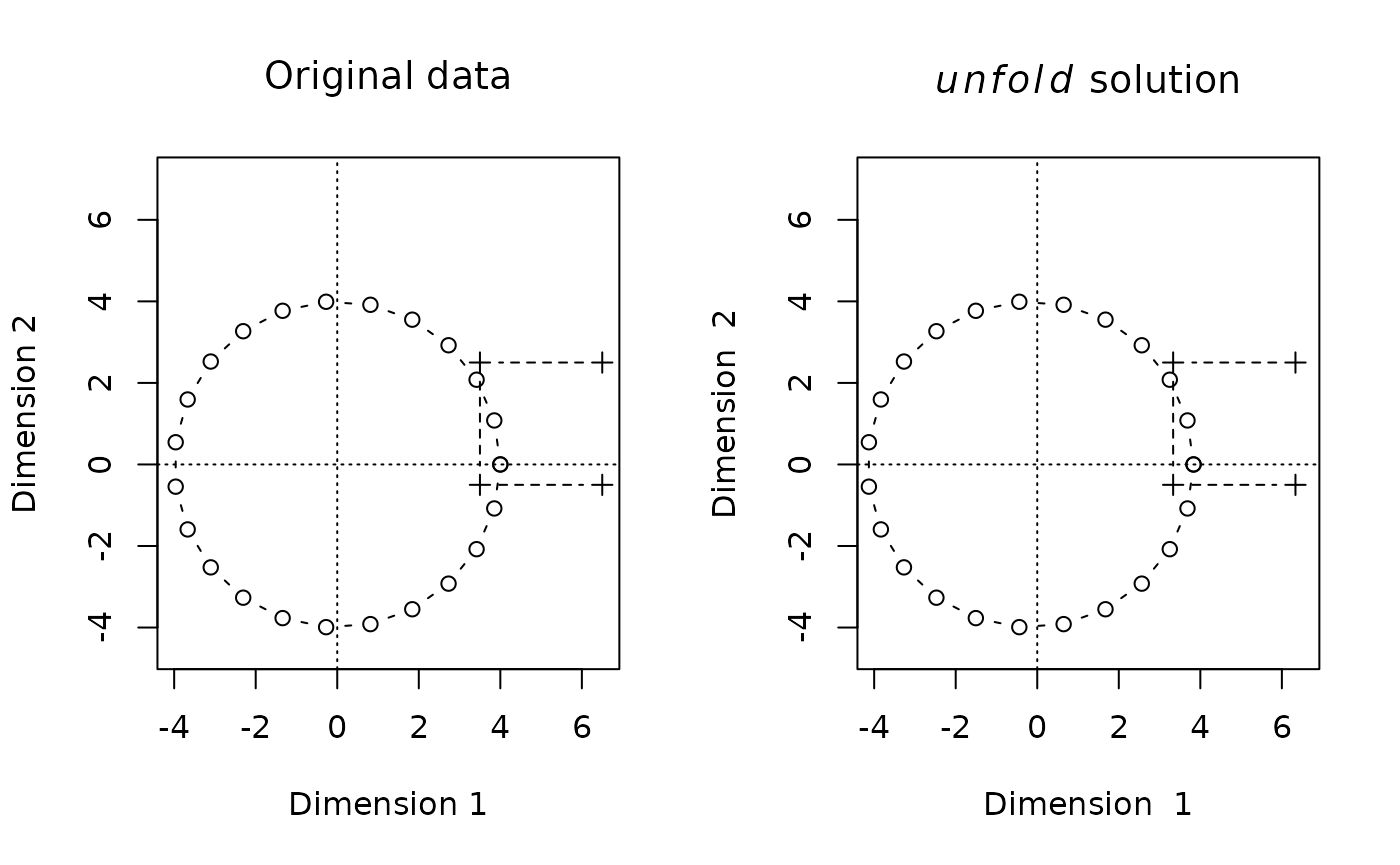

par(oldpar)

Curiously, Schönemann’s algorithm fails with a perfect circle:

r <- seq(from=0,to=2*pi,length=24)
a1_0 <- cos(r)*4 # NB: no random noise added here
a2_0 <- sin(r)*4
b1_0 <- c(.5,-.5,-.5,.5)*3 + 5
b2_0 <- c(.5,.5,-.5,-.5)*3 + 1
D1_0 <- outer(b1_0,a1_0,"-")
D2_0 <- outer(b2_0,a2_0,"-")
Dsq0 <- D1_0^2+D2_0^2
Dsq.uf0 <- unfold(Dsq0,squared=TRUE)
Dsq.uf0


2-dimensional unfolding solution

Group 1: 24 points
Group 2: 4 points

Stress: 0.2191948

The stress level indicates an imperfect fit, while the configuration within groups seems to be okay, the overall configuration is wrong:

biplot(Dsq.uf0,type="b")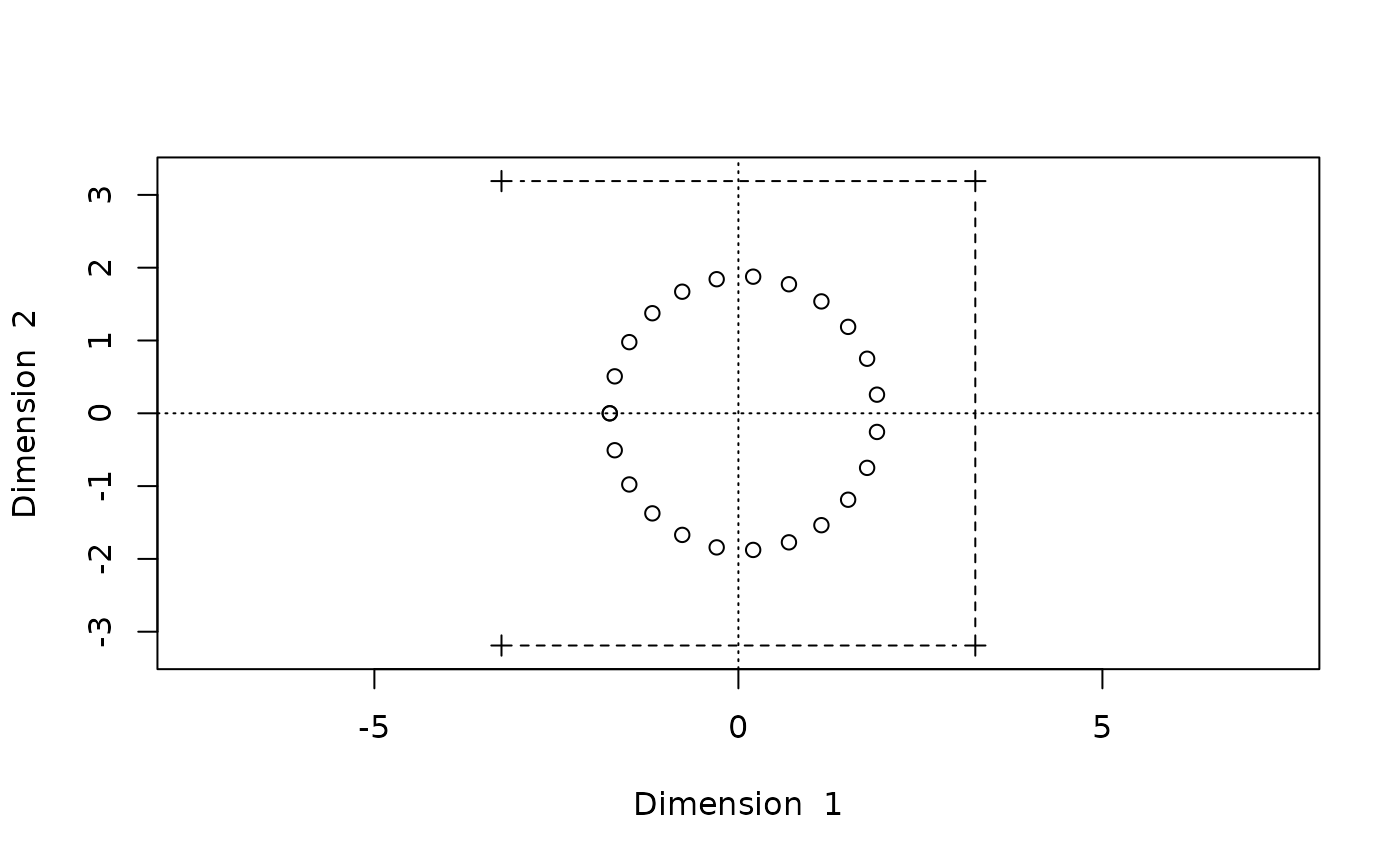

However, the iterative conjugate gradient method seems to work:

Dsq.uf0.cg<-unfold(Dsq,squared=TRUE,method="CG")


Stress for starting values 1.050001e-21
Stress after translation 4.538332e-22
Stress after rescaling 2.489772e-22
Gradient: 5.11866e-07 -1.502135e-06
Stress after rigid transformation 2.016861e-22
Gradient: -1.296438e-06 -1.010401e-06 1.289886e-06 1.826926e-07

Dsq.uf0.cg


2-dimensional unfolding solution

Group 1: 24 points
Group 2: 4 points

Stress: 1.773783e-22

We get a non-convergence warning, but the stress level is much lower and the reconstructed configuration looks okay:

biplot(Dsq.uf0.cg,type="b")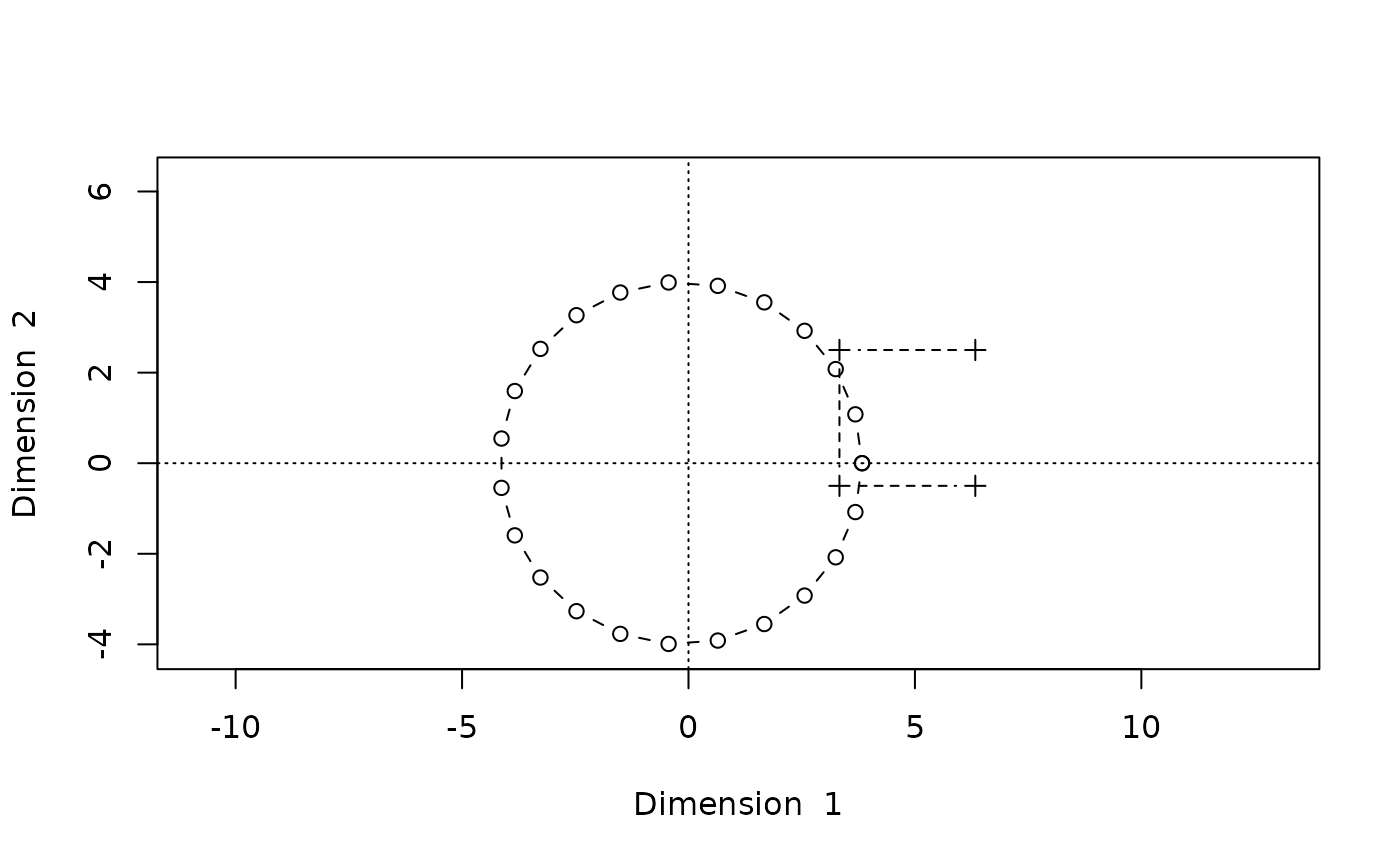

Less surprisingly, it is important to correctly indicate whether the input for unfold() consists of squared distances or un-squared distances.

Here we provide squared distances, but indicate that the distances are not squared.

Dsq.uf1 <- unfold(Dsq,squared=FALSE)
Dsq.uf1


3-dimensional unfolding solution

Group 1: 24 points
Group 2: 4 points

Stress: 0.1712989

We get an additional spurious dimension and the reconstruction of the points is distorted:

biplot(Dsq.uf1,type="b")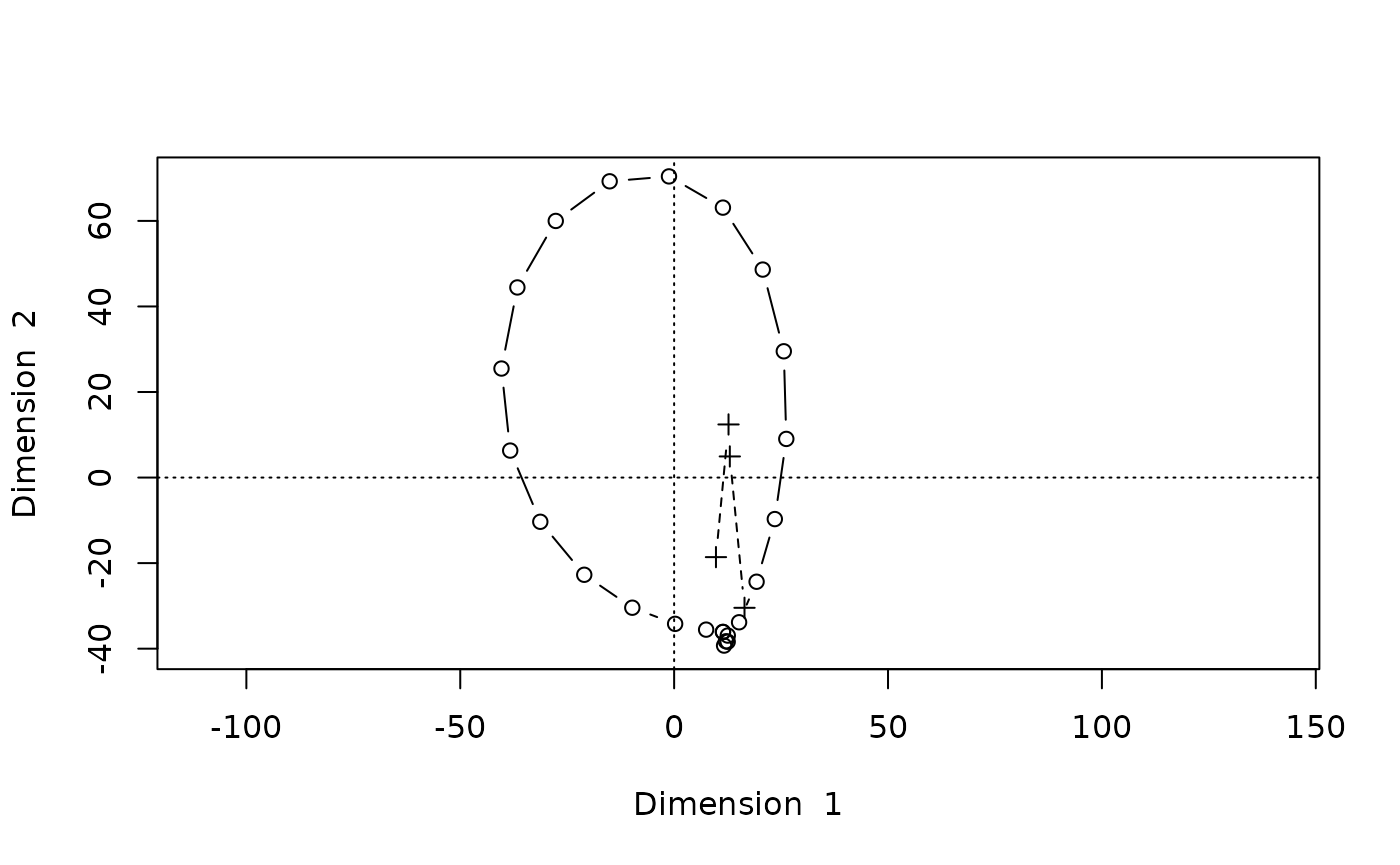

Here we provide non-squared distances, but indicate that the distances are squared.

Dsq.uf2 <- unfold(sqrt(Dsq),squared=TRUE)
Dsq.uf2


3-dimensional unfolding solution

Group 1: 24 points
Group 2: 4 points

Stress: 799461.7

Again we end up with a spurious additional dimension and a distorted configuration of the points:

biplot(Dsq.uf2,type="b")

Metric unfolding with “munfold”